Bacterial Population Growth Model with Runge-Kutta Method
Bacterial Population Growth Model with Runge-Kutta Method
DOI:
https://doi.org/10.63876/ijss.v1i3.23Keywords:
Population Growth Model, Bacteria, Runge-Kutta Method, Differential Equation, Logistic Model, Population Prediction, Numerical ApproachAbstract
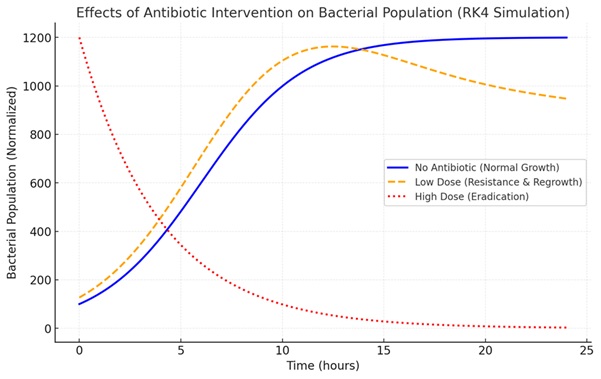
The bacterial population growth model is one way to understand the dynamics of microorganisms under various environmental conditions. This study aims to model the growth of bacterial populations using the Runge-Kutta method as a numerical approach to solve differential equations describing growth rates. This method was chosen because of its high accuracy in predicting the solution value at a given time interval compared to other numerical methods. In this study, a logistics model was applied that considered factors such as environmental capacity and the intrinsic growth rate of bacteria. The initial population data and model parameters were processed using the fourth-order Runge-Kutta method, which was then validated with analytical solutions or simulations based on experimental data. The results of the analysis show that this method is able to predict bacterial growth patterns with minimal error rates. In addition, this method is also flexible to be applied to scenarios with variable parameters, such as environmental changes or the influence of antibiotics. The conclusions of this study show that the Runge-Kutta method is an effective tool for modeling the dynamics of bacterial growth, providing a more accurate picture of population changes over time. These findings have the potential to support the development of strategies in various fields, such as biotechnology, waste treatment, and microorganism infection control. Further research is recommended to integrate other external factors to improve the accuracy of the model.
Downloads
References
M. Yousefi, S. M. Hoseini, E. V. Kulikov, E. V. Kharlitskaya, N. V. Petukhov, and N. G. Khomenets, “Dietary propionate administration improves growth performance, hepatic lipid deposition, and intestinal activity of digestive enzymes, inflammation, bacterial population, and antioxidant capacity in rainbow trout, Oncorhynchus mykiss,” Aquaculture, vol. 578, p. 740099, Jan. 2024, doi: https://doi.org/10.1016/j.aquaculture.2023.740099.
R. Wang, X. Yang, G. Li, W. Zheng, Z. Zou, and C. Sun, “Pattern and dynamics of methane/water two-phase flow in deep-shale illite nanoslits,” Int. J. Heat Fluid Flow, vol. 110, p. 109625, Dec. 2024, doi: https://doi.org/10.1016/j.ijheatfluidflow.2024.109625.
M. K. Hasan, X. Lei, A. Hlali, and Z. Bian, “Modelling capability factors of logistics industry based on ISM-MICMAC,” Heliyon, vol. 10, no. 22, p. e40539, Nov. 2024, doi: https://doi.org/10.1016/j.heliyon.2024.e40539.
D. F. Fernandes, M. C. Santos, A. C. Silva, and A. M. M. Lima, “Comparative study of CUDA-based parallel programming in C and Python for GPU acceleration of the 4th order Runge-Kutta method,” Nucl. Eng. Des., vol. 421, p. 113050, May 2024, doi: https://doi.org/10.1016/j.nucengdes.2024.113050.
W. J. de S. Gomes, A. T. Beck, and A. G. Garmbis, “Efficient Runge–Kutta solver for stochastic crack growth analysis,” Probabilistic Eng. Mech., vol. 74, p. 103503, Oct. 2023, doi: https://doi.org/10.1016/j.probengmech.2023.103503.
M. N. Azese, “Optimizing linear/non-linear Volterra-type integro-differential equations with Runge–Kutta 2 and 4 for time efficiency,” Sci. African, vol. 26, p. e02443, Dec. 2024, doi: https://doi.org/10.1016/j.sciaf.2024.e02443.
K. S. Nisar, M. Farman, M. Abdel-Aty, and J. Cao, “A review on epidemic models in sight of fractional calculus,” Alexandria Eng. J., vol. 75, pp. 81–113, Jul. 2023, doi: https://doi.org/10.1016/j.aej.2023.05.071.
K. Chen, B. Xiao, C. Wang, X. Liu, X. Zhang, and C. Xia, “FRKVF: High-accuracy motion interpolation for polishing operations using fourth-order Runge-Kutta and velocity flexibility planning,” Precis. Eng., vol. 90, pp. 122–140, Oct. 2024, doi: https://doi.org/10.1016/j.precisioneng.2024.08.008.
F. Dai and B. Liu, “Optimal control problem for a general reaction-diffusion eco-epidemiological model with disease in prey,” Appl. Math. Model., vol. 88, pp. 1–20, Dec. 2020, doi: https://doi.org/10.1016/j.apm.2020.06.040.
Y. Fu et al., “An enhanced machine learning-based prognostic prediction model for patients with AECOPD on invasive mechanical ventilation,” iScience, vol. 27, no. 12, p. 111230, Dec. 2024, doi: https://doi.org/10.1016/j.isci.2024.111230.
S. J. Seidel et al., “The overlooked effects of environmental impacts on root:shoot ratio in experiments and soil-crop models,” Sci. Total Environ., vol. 955, p. 176738, Dec. 2024, doi: https://doi.org/10.1016/j.scitotenv.2024.176738.
S. Arshad, S. F. Jaffer Hussain, S. Jayaram, V. P. Veeraraghavan, and M. I. Karobari, “Perspective on enhancing quality of life in oral cancer patients: Integrative approaches and comprehensive care,” Oral Oncol. Reports, vol. 11, p. 100633, Sep. 2024, doi: https://doi.org/10.1016/j.oor.2024.100633.
F. de J. Silerio-Vázquez, L. A. González-Burciaga, C. Antileo, C. M. Núñez-Núñez, and J. B. Proal-Nájera, “Photocatalytic degradation of antibiotics in water via TiO2-x: Research needs for technological advancements,” J. Hazard. Mater. Adv., vol. 16, p. 100506, Nov. 2024, doi: https://doi.org/10.1016/j.hazadv.2024.100506.
A. Chen et al., “Applications and synergistic degradation mechanisms of nZVI-modified biochar for the remediation of organic polluted soil and water: A review,” Sci. Total Environ., vol. 911, p. 168548, Feb. 2024, doi: https://doi.org/10.1016/j.scitotenv.2023.168548.
Y. Y. Liang, “Review of analytical and numerical modeling for pressure retarded osmosis membrane systems,” Desalination, vol. 560, p. 116655, Aug. 2023, doi: https://doi.org/10.1016/j.desal.2023.116655.
F. Zare, A. J. Jakeman, S. Elsawah, and J. H. A. Guillaume, “Bridging practice and science in socio-environmental systems research and modelling: A design science approach,” Ecol. Modell., vol. 492, p. 110719, Jun. 2024, doi: https://doi.org/10.1016/j.ecolmodel.2024.110719.
J. Sun and Y. Wang, “Modeling the contribution of grit, hope to perceptions of creativity among Chinese college EFL teachers,” Think. Ski. Creat., vol. 54, p. 101665, Dec. 2024, doi: https://doi.org/10.1016/j.tsc.2024.101665.
V. A. Khoa, P. M. Quan, J. Allen, and K. W. Blayneh, “Efficient relaxation scheme for the SIR and related compartmental models,” J. Comput. Sci., vol. 84, p. 102478, Jan. 2025, doi: https://doi.org/10.1016/j.jocs.2024.102478.
Y. Zhang et al., “Global daily mask use estimation in the pandemic and its post environmental health risks: Analysis based on a validated dynamic mathematical model,” J. Hazard. Mater., vol. 473, p. 134572, Jul. 2024, doi: https://doi.org/10.1016/j.jhazmat.2024.134572.
A. S. V. Ravi Kanth and S. Devi, “A computational approach for numerical simulations of the fractal–fractional autoimmune disease model,” Chaos, Solitons & Fractals, vol. 165, p. 112829, Dec. 2022, doi: https://doi.org/10.1016/j.chaos.2022.112829.
B. Chen and F. Solis, “Discretizations of nonlinear differential equations using explicit finite order methods,” J. Comput. Appl. Math., vol. 90, no. 2, pp. 171–183, Apr. 1998, doi: https://doi.org/10.1016/S0377-0427(98)00017-X.
J. Zhang, L. Zhang, and X. Liu, “Supplementary irrigation with ceramic emitter promotes Platycladus orientalis growth by enhancing soil bacterial α diversity under extremely high-temperature,” Agric. Water Manag., vol. 301, p. 108958, Aug. 2024, doi: https://doi.org/10.1016/j.agwat.2024.108958.